🐥 Quick Sort
Quick Sort는 거의 모든 정렬 알고리즘보다 빠른 특징을 가지고 있기 때문에 라이브러리에서의 정렬은 대부분 Quick Sort를 바탕으로 만들어져있다.
Quick Sort는 매번 Pivot이라는 원소를 하나 선택하고 Pivot을 제자리로 보내는 작업을 반복한다. Pivot을 제자리로 보낸다는 말의 의미는 Pivot의 왼쪽에는 Pivot보다 작은 원소들을, Pivot의 오른쪽에는 Pivot보다 큰 원소들을 위치시킨다는 것이다.
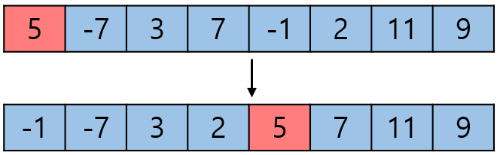
가장 왼쪽에 있는 원소인 5를 Pivot으로 잡는다면 Pivot의 제자리는 위와 같다. Pivot을 기준으로 왼쪽은 Pivot보다 작은 원소들이, 오른쪽은 Pivot보다 큰 원소들이 있는 것을 볼 수 있다.
자세한 동작과정을 살펴보면 다음과 같다. Pivot을 제외한 양쪽 끝에 포인터를 두고 적절하게 스왑을 해주면 된다. 왼쪽 포인터 l, 오른쪽 포인터 r을 둔다.
l은 Pivot보다 큰 값이 나올 때까지 오른쪽으로 이동하고 r은 Pivot보다 작은 값이 나올 때까지 왼쪽으로 이동한다.
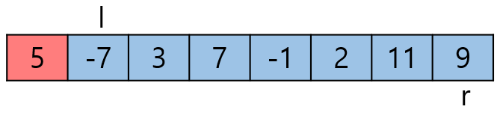
초기 상태

l이동 후
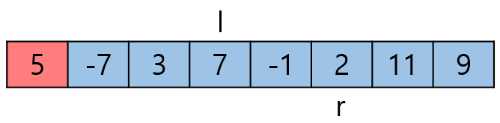
r이동 후
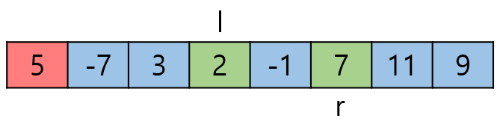
l과 r의 이동이 멈췄고 l이 r보다 작거나 같다면 두 원소를 스왑한다.
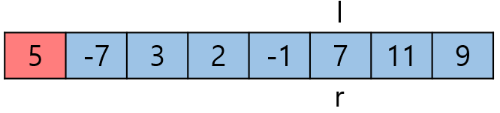
l 이동 후

r 이동 후
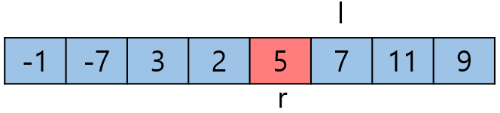
l과 r의 이동이 멈췄고 l이 r보다 크기 때문에 r에 위치한 원소와 Pivot의 자리를 바꾼다. 이로써 Pivot의 제자리를 찾을 수 있다.
💻 구현(C++)
2751번: 수 정렬하기 2
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000,000)이 주어진다. 둘째 줄부터 N개의 줄에는 수가 주어진다. 이 수는 절댓값이 1,000,000보다 작거나 같은 정수이다. 수는 중복되지 않는다.
www.acmicpc.net
#include <iostream>
#define MAX 1000005
using namespace std;
int N;
int arr[MAX];
void quick_sort(int st, int en) {
if (en <= st + 1) return; // base condition
int pivot = arr[st]; // 피벗
int l = st + 1; // 왼쪽 포인터
int r = en - 1; // 오른쪽 포인터
while (true) {
while (l <= r && arr[l] <= pivot) l++;
while (l <= r && arr[r] >= pivot) r--;
if (l > r) break;
swap(arr[l], arr[r]);
}
swap(arr[st], arr[r]);
quick_sort(st, r);
quick_sort(r + 1, en);
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> N;
for (int i = 0; i < N; i++) {
cin >> arr[i];
}
quick_sort(0, N);
for (int i = 0; i < N; i++) {
cout << arr[i] << '\n';
}
return 0;
}
⏱ 시간복잡도
Quick Sort의 과정과 시간복잡도를 알아보자.
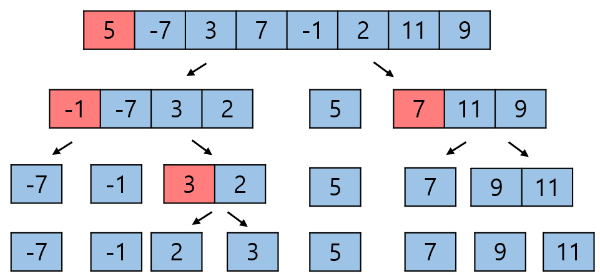
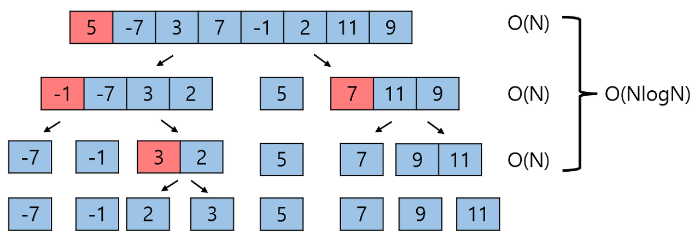
Pivot을 제자리로 보내는 시간복잡도는 리스트의 크기에 비례한다. 즉 각 단계마다 O(N)이 필요하다.
Pivot이 매번 정가운데 위치해서 리스트를 둘로 쪼갠다면 단계는 logN이 될 것이다.
이 경우 Quick Sort의 전체 시간 복잡도는 O(NlogN)이 된다.
💻 최악의 경우
굉장히 좋아보이는 Quick Sort에는 치명적인 단점이 있다. 다음의 예시를 보자.
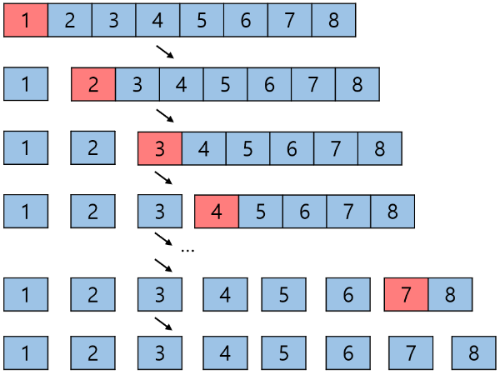
1 2 3 4 5 6 7 8 을 Quick Sort를 이용하여 정렬하면 매번 선택되는 Pivot은 가장 왼쪽에 위치할 것이고 이 때문에 단계는 logN이 아닌 N번의 단계가 된다.

따라서 이때의 시간복잡도는 O(N²)이 된다.
앞에서 대부분의 라이브러리의 정렬 알고리즘은 Quick Sort로 구현되어 있다고 했다. 그런데 최악의 경우에 O(N²)인 Quick Sort를 사용하는게 이해가 안될 수도 있지만 내부적으로 다양한 처리를 한다.
예를 들면 Pivot을 랜덤하게 고르거나, Pivot의 후보를 정하고 후보의 중앙값을 Pivot으로 정하기도 한다. 최악의 경우에도 O(NlongN)을 보장하기 위해서 일정 깊이 이상 들어가면 Quick Sort 대신 Heap Sort로 정렬한다.
📃 정리
- Quick Sort의 평균 시간복잡도는 O(NlogN)
- Quick Sort의 최악의 시간복잡도는 O(N²)
- Quick Sort는 In-Place(추가적인 공간이 필요하지 않음) Sort
- cache hit rate가 높음
참고
[1] https://www.youtube.com/watch?v=59fZkZO0Bo4&t=68s
[2] https://blog.encrypted.gg/955
🐥 Quick Sort
Quick Sort는 거의 모든 정렬 알고리즘보다 빠른 특징을 가지고 있기 때문에 라이브러리에서의 정렬은 대부분 Quick Sort를 바탕으로 만들어져있다.
Quick Sort는 매번 Pivot이라는 원소를 하나 선택하고 Pivot을 제자리로 보내는 작업을 반복한다. Pivot을 제자리로 보낸다는 말의 의미는 Pivot의 왼쪽에는 Pivot보다 작은 원소들을, Pivot의 오른쪽에는 Pivot보다 큰 원소들을 위치시킨다는 것이다.

가장 왼쪽에 있는 원소인 5를 Pivot으로 잡는다면 Pivot의 제자리는 위와 같다. Pivot을 기준으로 왼쪽은 Pivot보다 작은 원소들이, 오른쪽은 Pivot보다 큰 원소들이 있는 것을 볼 수 있다.
자세한 동작과정을 살펴보면 다음과 같다. Pivot을 제외한 양쪽 끝에 포인터를 두고 적절하게 스왑을 해주면 된다. 왼쪽 포인터 l, 오른쪽 포인터 r을 둔다.
l은 Pivot보다 큰 값이 나올 때까지 오른쪽으로 이동하고 r은 Pivot보다 작은 값이 나올 때까지 왼쪽으로 이동한다.

초기 상태

l이동 후

r이동 후

l과 r의 이동이 멈췄고 l이 r보다 작거나 같다면 두 원소를 스왑한다.

l 이동 후

r 이동 후

l과 r의 이동이 멈췄고 l이 r보다 크기 때문에 r에 위치한 원소와 Pivot의 자리를 바꾼다. 이로써 Pivot의 제자리를 찾을 수 있다.
💻 구현(C++)
2751번: 수 정렬하기 2
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000,000)이 주어진다. 둘째 줄부터 N개의 줄에는 수가 주어진다. 이 수는 절댓값이 1,000,000보다 작거나 같은 정수이다. 수는 중복되지 않는다.
www.acmicpc.net
#include <iostream>
#define MAX 1000005
using namespace std;
int N;
int arr[MAX];
void quick_sort(int st, int en) {
if (en <= st + 1) return; // base condition
int pivot = arr[st]; // 피벗
int l = st + 1; // 왼쪽 포인터
int r = en - 1; // 오른쪽 포인터
while (true) {
while (l <= r && arr[l] <= pivot) l++;
while (l <= r && arr[r] >= pivot) r--;
if (l > r) break;
swap(arr[l], arr[r]);
}
swap(arr[st], arr[r]);
quick_sort(st, r);
quick_sort(r + 1, en);
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> N;
for (int i = 0; i < N; i++) {
cin >> arr[i];
}
quick_sort(0, N);
for (int i = 0; i < N; i++) {
cout << arr[i] << '\n';
}
return 0;
}
⏱ 시간복잡도
Quick Sort의 과정과 시간복잡도를 알아보자.


Pivot을 제자리로 보내는 시간복잡도는 리스트의 크기에 비례한다. 즉 각 단계마다 O(N)이 필요하다.
Pivot이 매번 정가운데 위치해서 리스트를 둘로 쪼갠다면 단계는 logN이 될 것이다.
이 경우 Quick Sort의 전체 시간 복잡도는 O(NlogN)이 된다.
💻 최악의 경우
굉장히 좋아보이는 Quick Sort에는 치명적인 단점이 있다. 다음의 예시를 보자.

1 2 3 4 5 6 7 8 을 Quick Sort를 이용하여 정렬하면 매번 선택되는 Pivot은 가장 왼쪽에 위치할 것이고 이 때문에 단계는 logN이 아닌 N번의 단계가 된다.

따라서 이때의 시간복잡도는 O(N²)이 된다.
앞에서 대부분의 라이브러리의 정렬 알고리즘은 Quick Sort로 구현되어 있다고 했다. 그런데 최악의 경우에 O(N²)인 Quick Sort를 사용하는게 이해가 안될 수도 있지만 내부적으로 다양한 처리를 한다.
예를 들면 Pivot을 랜덤하게 고르거나, Pivot의 후보를 정하고 후보의 중앙값을 Pivot으로 정하기도 한다. 최악의 경우에도 O(NlongN)을 보장하기 위해서 일정 깊이 이상 들어가면 Quick Sort 대신 Heap Sort로 정렬한다.
📃 정리
- Quick Sort의 평균 시간복잡도는 O(NlogN)
- Quick Sort의 최악의 시간복잡도는 O(N²)
- Quick Sort는 In-Place(추가적인 공간이 필요하지 않음) Sort
- cache hit rate가 높음
참고
[1] https://www.youtube.com/watch?v=59fZkZO0Bo4&t=68s
[2] https://blog.encrypted.gg/955
