📌 Intro
0-1 BFS란 가중치가 0과 1로만 주어진 그래프에서 최단 경로를 찾는 알고리즘인데, 이에 대해 자세하게 알아보도록 하자.
📌 0-1 BFS
보통 최단 경로를 이야기할 때는 다익스트라 알고리즘이 가장 빠르게 동작한다고 알고 있을 것이다. 하지만 가중치가 0과 1로만 주어진 그래프에서는 다익스트라 알고리즘보다 0-1 BFS가 더빠르게 동작한다. 다익스트라 알고리즘의 시간 복잡도는 O(ElogV)이지만 0-1 BFS는 O(V+E)의 시간 복잡도를 가지기 때문이다.
먼저 0-1 BFS의 동작 원리를 살펴보면 다음과 같다.
- deque front에서 현재 노드를 꺼낸다.
- 인접 노드를 체크한다.
- 현재 노드까지의 비용 + 인접 노드로의 비용 < 인접 노드까지 소요된 비용 의 경우 인접 노드로의 비용을 갱신해준다.
- 인접 노드로의 가중치가 0이라면 deque의 front에 삽입, 1이라면 deque의 back에 삽입한다.
- deque가 empty될 때까지 위 과정을 반복한다.
보다시피 queue로 구현하는 일반적인 BFS와는 달리 deque이라는 자료구조를 사용하여 0-1 BFS를 구현할 수 있다. deque이라는 자료구조는 앞, 뒤에서 삽입과 삭제를 모두 할 수 있는 자료구조다.
여기서 가장 중요한 점은 "가중치가 0이면 front에 1이면 back에 삽입"한다는 것이다.
0-1 BFS의 시간 복잡도가 O(V+E)가 되는 것을 살펴보면, 비용이 적은 경로부터 탐색하기 때문에 특정 간선을 2번을 초과하여 지나가는 경우는 없다. 이와 같은 의미에서 같은 정점 역시 2번을 초과하여 방문하지 않기 때문에 deque의 크기는 최대 |V|가 된다.
따라서 0-1 BFS의 시간 복잡도는 O(V) + O(E) = O(V+E)가 된다.
STEP 0
다음과 같은 그래프에서 0-1 BFS가 어떻게 동작하는지 살펴보도록 하자. 출발 노드는 A라고 가정하자.
현재 처리중인 노드와 간선은 하늘색으로, 방문한 노드는 회색으로 표시하였다.
또 같은 상황의 노드가 여러개인 경우 알파벳이 더 빠른 노드를 먼저 처리하도록 했다.
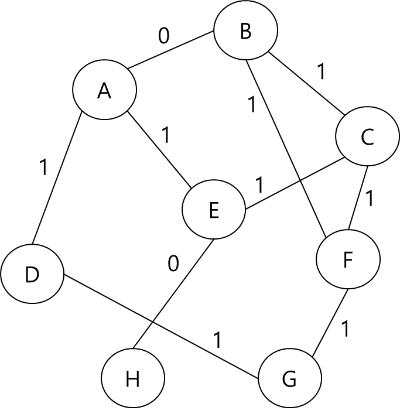
STEP 1
출발 노드 A와 인접한 노드는 B, D, E다. 거리 리스트에서 B, D, E로 가는 가중치를 갱신해준다.
B로 가는 간선의 가중치는 0이기 때문에 덱의 front에 추가해준다. D, E로 가는 간선의 가중치는 1이기 때문에 덱의 back에 추가해준다.



STEP 2
덱의 가장 앞에 있는 B노드를 꺼낸다. B와 인접한 노드 중 방문하지 않은 노드는 C와 F다. 거리 리스트에서 C와 F로 가는 가중치를 갱신해준다.
C와 F로 가는 두 간선의 가중치가 모두 1이기 때문에 덱의 back에 추가해준다.



STEP 3
덱의 가장 앞에 있는 D노드를 꺼낸다. D와 인접한 노드 중 방문하지 않은 노드는 G이다. 거리 리스트에서 G로 가는 가중치를 갱신해준다.
G로 가는 간선의 가중치가 1이기 때문에 덱의 back에 추가해준다.



STEP 4
덱의 가장 앞에 있는 E노드를 꺼낸다. E와 인접한 노드 중 방문하지 않은 노드는 C와 H다. 거리 리스트에 저장된 값이 E를 통해 방문하는 값보다 작기 때문에 갱신하지 않는다.
H로 가는 간선의 가중치는 0이기 때문에 덱의 front에 추가해주고, C로 가는 간선의 가중치는 1이기 때문에 덱의 back에 추가해준다.
이 때 덱에 이미 C가 있지만 또 추가해줘도 상관없는 이유는 결국 처음에 C노드를 꺼냈을 때 주변을 살펴보기 때문에 C노드를 다시 추가해도 괜찮은 것이다.
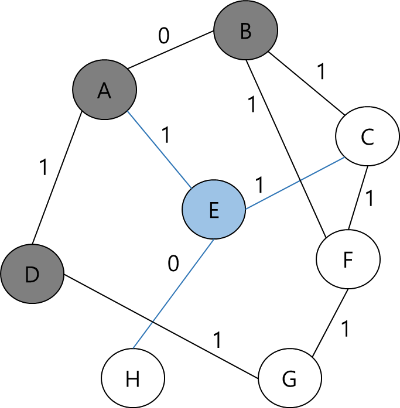


STEP 5
덱의 가장 앞에 있는 H노드를 꺼낸다. H와 인접한 노드 중 방문하지 않은 노드는 없기 때문에 다른 일은 일어나지 않는다.
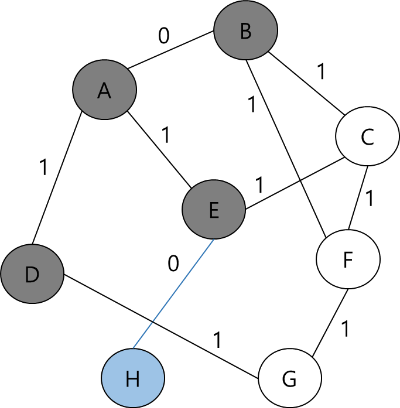


STEP 6
덱의 가장 앞에 있는 C노드를 꺼낸다. C와 인접한 노드 중 방문하지 않은 노드는 F다. 거리 리스트에 저장된 값이 C를 통해 F 방문하는 값보다 작기 때문에 갱신하지 않는다.
F로 가는 간선의 가중치가 1이기 때문에 덱의 back에 추가해준다.



STEP 7
덱의 가장 앞에 있는 F노드를 꺼낸다. F와 인접한 노드 중 방문하지 않은 노드는 G다. 거리 리스트에 저장된 값과 F를 통해 G를 방문하는 값이 같기 때문에 갱신하지 않는다.
G로 가는 간선의 가중치가 1이기 때문에 덱의 back에 추가해준다.
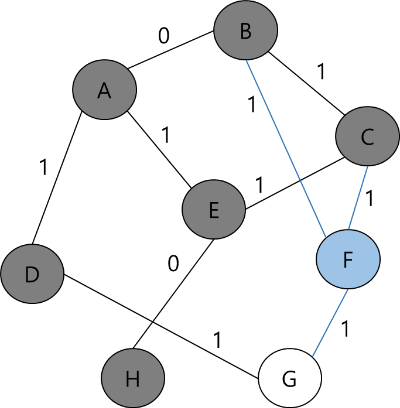


STEP 8
덱의 가장 앞에 있는 G노드를 꺼낸다. G노드와 인접한 노드 중 방문하지 않은 노드는 없다. 따라서 다른 일은 일어나지 않는다.



STEP 9..
덱에서 노드를 꺼낸 뒤 인접 노드를 살펴봐도 방문하지 않은 노드는 없기 때문에 덱에 원소가 없을 때까지 노드를 꺼내는 일만 반복한다.
결과적으로 A노드에서 다른 노드로 방문하는 최소 비용은 다음과 같을 것이다.

📌 Details
예시로 든 그래프를 쭉 살펴보면 알겠지만 모든 간선을 2번을 넘게 방문하지 않는다. 또, 노드의 경우도 2번을 넘게 방문하지 않는다.
따라서 앞에서 살펴본 0-1 BFS의 시간 복잡도는 O(V+E)가 되는 것을 증명할 수 있다.
📌 관련 문제
📌 참고
[1] https://nicotina04.tistory.com/168
[2] https://chan9.tistory.com/120
