[알고리즘] 크루스칼(Kruskal) 알고리즘

📌 Intro

크루스칼 알고리즘은 그래프에서 모든 정점들을 가장 적은 비용으로 연결하는 방법을 찾는 알고리즘이다. 다르게 말하면 최소 신장 트리를 찾는 알고리즘이다.
신장트리는 그래프가 있을 때 모든 노드를 포함하면서 사이클이 존재하지 않는 부분 그래프를 말하고, 최소 신장트리는 이러한 신장 트리들 중 비용이 가장 적은 신장 트리를 말한다.

📌 크루스칼 알고리즘

앞에서 말한 것처럼 크루스칼 알고리즘을 사용하면 그래프 내에서 가장 적은 비용으로 모든 노드를 연결하는 방법을 찾을 수 있다.
크루스칼 알고리즘은 모든 간선에 대해 정렬을 수행한 뒤 가장 거리가 짧은 간선부터 집합에 포함시키면서 진행을 하기 때문에 그리디 알고리즘으로 분류된다.

 

구체적인 알고리즘은 다음과 같다.

1. 간선 데이터를 비용에 따라 오름차순 정렬한다.
2. 간선을 하나씩 확인하며 현재의 간선이 사이클을 발생시키는지 확인한다. 만약 사이클이 발생하는 경우 최소 신장 트리에 추가하지 않고, 사이클이 발생하지 않는다면 최소 신장 트리에 추가해준다.
3. 모든 간선에 대해 2번 과정을 반복한다.

STEP 0

다음과 같은 예시를 통해 최소 신장 트리를 구해보도록 하자. 크루스칼 알고리즘을 시작하기 전에 그래프에 존재하는 모든 간선을 비용에 따라 정렬해줘야 한다. 하지만 가독성을 위해 표를 작성할 때는 노드가 작은 것부터 나타냈다. 확인한 간선 중 최소 신장 트리로 선택된 간선은 하늘색으로 표시할 것이고, 선택하지 않은 간선은 점선으로 표시할 것이다.

STEP 1

 

가장 비용이 적은 (2, 6)사이 간선을 선택한다. 이 때 사이클이 만들어지지 않기 때문에 최소 신장 트리에 추가한다.

STEP 2

 

그 다음으로 가장 비용이 적은 간선인 (2, 3)사이 간선을 선택한다. 이 때도 사이클이 만들어지지 않기 때문에 최소 신장 트리에 추가한다.

STEP 3

 

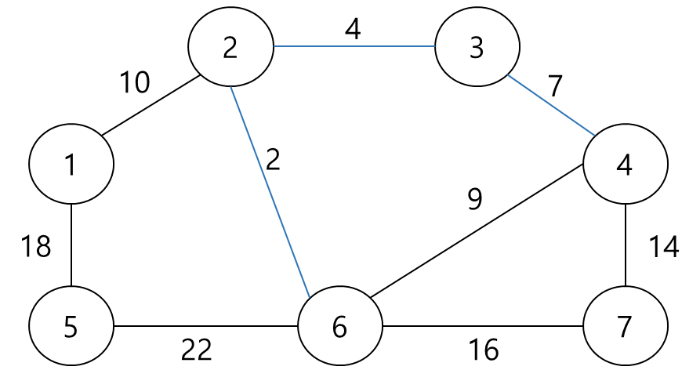
그 다음으로 가장 비용이 적은 간선인 (3, 4)사이 간선을 선택한다. 이 때도 사이클이 만들어지지 않기 때문에 최소 신장 트리에 추가한다.

STEP 4

 

그 다음으로 가장 비용이 적은 간선인 (4, 6)사이 간선을 선택한다. 이 때는 사이클이 만들어지기 때문에 최소 신장 트리에 추가하지 않는다.

STEP 5

 

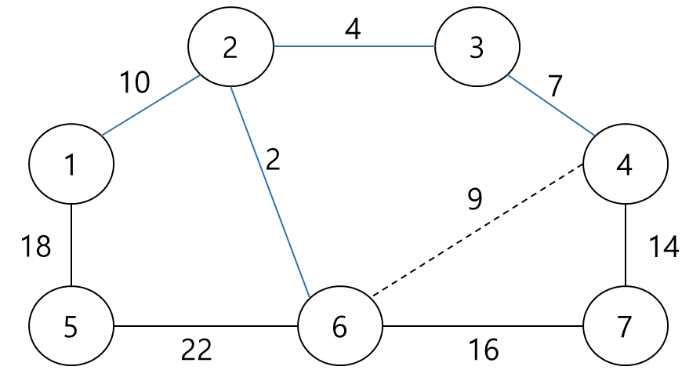
그 다음으로 가장 비용이 적은 간선인 (1, 2)사이 간선을 선택한다. 이 때는 사이클이 만들어지지 않기 때문에 최소 신장 트리에 추가한다.

STEP 6

 

그 다음으로 가장 비용이 적은 간선인 (4, 6)사이 간선을 선택한다. 이 때는 사이클이 만들어지지 않기 때문에 최소 신장 트리에 추가한다.

STEP 7

 

그 다음으로 가장 비용이 적은 간선인 (6, 7)사이 간선을 선택한다. 이 때는 사이클이 만들어지기 때문에 최소 신장 트리에 추가하지 않는다.

STEP 8

 

그 다음으로 가장 비용이 적은 간선인 (1, 5)사이 간선을 선택한다. 이 때는 사이클이 만들어지지 않기 때문에 최소 신장 트리에 추가한다.

STEP 9

 

그 다음으로 가장 비용이 적은 간선인 (5, 6)사이 간선을 선택한다. 이 때는 사이클이 만들어지기 때문에 최소 신장 트리에 추가하지 않는다.

크루스칼 알고리즘을 통해 만들어진 최소 신장트리는 위와 같은 그래프가 될 것이다.

📌 구현(C++)

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

// 노드의 개수(V)와 간선(Union 연산)의 개수(E)
// 노드의 개수는 최대 100,000개라고 가정
int v, e;
int parent[100001]; // 부모 테이블 초기화
// 모든 간선을 담을 리스트와, 최종 비용을 담을 변수
vector<pair<int, pair<int, int> > > edges;
int result = 0;

// 특정 원소가 속한 집합을 찾기
int findParent(int x) {
    // 루트 노드가 아니라면, 루트 노드를 찾을 때까지 재귀적으로 호출
    if (x == parent[x]) return x;
    return parent[x] = findParent(parent[x]);
}

// 두 원소가 속한 집합을 합치기
void unionParent(int a, int b) {
    a = findParent(a);
    b = findParent(b);
    if (a < b) parent[b] = a;
    else parent[a] = b;
}

int main(void) {
    cin >> v >> e;

    // 부모 테이블상에서, 부모를 자기 자신으로 초기화
    for (int i = 1; i <= v; i++) {
        parent[i] = i;
    }

    // 모든 간선에 대한 정보를 입력 받기
    for (int i = 0; i < e; i++) {
        int a, b, cost;
        cin >> a >> b >> cost;
        // 비용순으로 정렬하기 위해서 튜플의 첫 번째 원소를 비용으로 설정
        edges.push_back({cost, {a, b}});
    }

    // 간선을 비용순으로 정렬
    sort(edges.begin(), edges.end());

    // 간선을 하나씩 확인하며
    for (int i = 0; i < edges.size(); i++) {
        int cost = edges[i].first;
        int a = edges[i].second.first;
        int b = edges[i].second.second;
        // 사이클이 발생하지 않는 경우에만 집합에 포함
        if (findParent(a) != findParent(b)) {
            unionParent(a, b);
            result += cost;
        }
    }

    // 최소 신장 트리 비용 출력
    cout << result << '\n';
}

 

 

📌 관련문제

1197번: 최소 스패닝 트리

1922번: 네트워크 연결

📌 참고

[1] 이것이 취업을 위한 코딩테스트다 with 파이썬
[2] https://chanhuiseok.github.io/posts/algo-33/