문제
계단 오르기 게임은 계단 아래 시작점부터 계단 꼭대기에 위치한 도착점까지 가는 게임이다. <그림 1>과 같이 각각의 계단에는 일정한 점수가 쓰여 있는데 계단을 밟으면 그 계단에 쓰여 있는 점수를 얻게 된다.
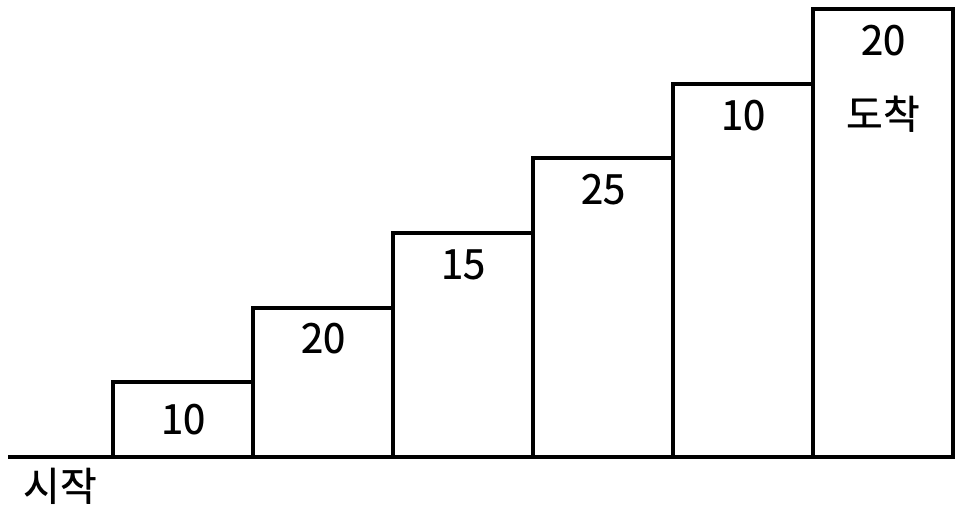
<그림 1>
예를 들어 <그림 2>와 같이 시작점에서부터 첫 번째, 두 번째, 네 번째, 여섯 번째 계단을 밟아 도착점에 도달하면 총 점수는 10 + 20 + 25 + 20 = 75점이 된다.
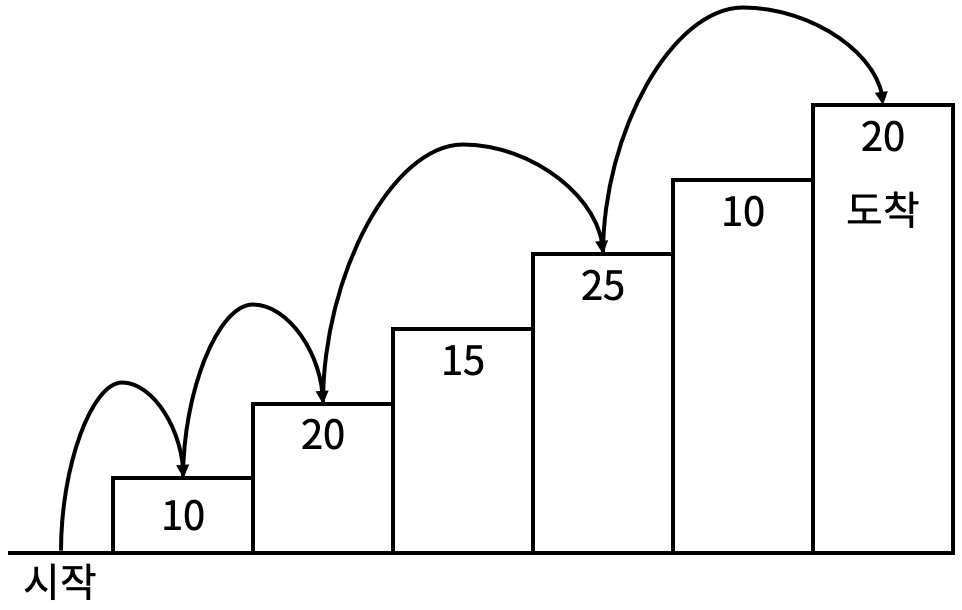
<그림 2>
계단 오르는 데는 다음과 같은 규칙이 있다.
- 계단은 한 번에 한 계단씩 또는 두 계단씩 오를 수 있다. 즉, 한 계단을 밟으면서 이어서 다음 계단이나, 다음 다음 계단으로 오를 수 있다.
- 연속된 세 개의 계단을 모두 밟아서는 안 된다. 단, 시작점은 계단에 포함되지 않는다.
- 마지막 도착 계단은 반드시 밟아야 한다.
따라서 첫 번째 계단을 밟고 이어 두 번째 계단이나, 세 번째 계단으로 오를 수 있다. 하지만, 첫 번째 계단을 밟고 이어 네 번째 계단으로 올라가거나, 첫 번째, 두 번째, 세 번째 계단을 연속해서 모두 밟을 수는 없다.
각 계단에 쓰여 있는 점수가 주어질 때 이 게임에서 얻을 수 있는 총 점수의 최댓값을 구하는 프로그램을 작성하시오.
입력
입력의 첫째 줄에 계단의 개수가 주어진다.
둘째 줄부터 한 줄에 하나씩 제일 아래에 놓인 계단부터 순서대로 각 계단에 쓰여 있는 점수가 주어진다. 계단의 개수는 300이하의 자연수이고, 계단에 쓰여 있는 점수는 10,000이하의 자연수이다.
출력
첫째 줄에 계단 오르기 게임에서 얻을 수 있는 총 점수의 최댓값을 출력한다.
풀이
DP를 이용하여 풀이하였다.
DP의 경우 점화식을 만드는 것이 가자 ㅇ중요하다.
i번째 계단에 올라올 수 있는 경우의 수는 두 가지이다.
- i-2번째 계단을 밟고 2칸을 넘어 i번째 계단으로 올라오는 경우
- i-3번째 계단을 밟고 2칸을 넘어 i-1번째 계단을 밟은 뒤 i번째 계단으로 올라오는 경우
1번의 점화식은 dp[i - 2] + stair[i] 가 된다.
2번의 점화식은 dp[i - 3] + stair[i - 1] + stair[i] 가 된다.
위 두 가지 값 중 더 큰 것을 dp[i]에 넣어주면 된다.
위의 점화식은 i가 4부터 가능(3도 가능하긴 하다.)하기 때문에
dp[1] 에는 stair[1] 값을,
dp[2] 에는 stair[1] + stair[2] 와 stair[1] 중 큰 값을,
dp[3] 에는 stair[1] + stair[3] 과 stair[2] + stair[3] 중 큰 값으로 초기화를 시켜주어야 한다.
코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int n;
int dp[301];
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n;
vector<int> stair(n + 1);
for (int i = 1; i <= n; i++) {
cin >> stair[i];
}
int curLocation = 0;
int stairs = 0;
dp[0] = 0;
dp[1] = stair[1];
dp[2] = max(stair[1] + stair[2], stair[2]);
dp[3] = max(stair[1] + stair[3], stair[2] + stair[3]);
for (int i = 4; i <= n; i++) {
dp[i] = max(dp[i - 2] + stair[i], dp[i - 3] + stair[i - 1] + stair[i]);
}
cout << dp[n];
}
|
cs |
메모
이번 DP문제를 풀면서 DP는 점화식을 만드는 것이 굉장히 중요하다는 생각이 들었다.
점화식을 만들게 되면 코딩이 조금 더 쉬워지고 직관적으로 이해할 수 있다.
